Hello guys, if you are preparing for technical interview for Software Development job then you must prepare well for Data Structure and Algorithms. It is often the difference between selection and non-selection and when it comes to Data Structure, binary search tree is one of the tough topic to master. In the past, I have shared 100+ data structure questions and 40+ binary tree questions and today, I am going to share one of the popular theory or concept questions related to binary tree data structure. The Tree data structure is one of the essential data structures, but unfortunately, many programmers don't pay enough attention to learning Trees, particularly advanced tree data structures like balanced trees like AVL and Red-Black tree.
Many of them think that knowing just array and the linked list is enough for programming interviews, but when they face questions about a tree, like the difference between binary tree and binary search tree, or the difference between binary search tree and a self-balanced tree-like AVL tree or Red-Black tree, they become speechless.
Only a few candidates know about Tries, another specialized data structure based upon a tree. Those rare candidates who have good knowledge of different types of trees, like a binary tree (BT), binary search tree (BST), self-balanced tree-like AVL, and Red-Black Tree and Tries, often do well on their programming interviews and also turns about to be a better developer than others.
In this article, I'll teach you about what is a tree data structure, what is a binary tree, what is binary search tree, what is a balanced tree and explain to you the fundamental difference between binary tree and binary search tree as well as the difference between binary tree and balanced tree and finally difference between different types of balanced tree-like AVL and Red-black tree.
Btw, If you are not familiar with fundamental data structures like an array, linked list, tree, and hash table, then I suggest you first go through a comprehensive course on Data Structure like Data Structures and Algorithms: Deep Dive Using Java on Udemy. It's essential for every programmer to have a solid understanding of these data structures as they are the basis of writing programs.
Only a few candidates know about Tries, another specialized data structure based upon a tree. Those rare candidates who have good knowledge of different types of trees, like a binary tree (BT), binary search tree (BST), self-balanced tree-like AVL, and Red-Black Tree and Tries, often do well on their programming interviews and also turns about to be a better developer than others.
In this article, I'll teach you about what is a tree data structure, what is a binary tree, what is binary search tree, what is a balanced tree and explain to you the fundamental difference between binary tree and binary search tree as well as the difference between binary tree and balanced tree and finally difference between different types of balanced tree-like AVL and Red-black tree.
Btw, If you are not familiar with fundamental data structures like an array, linked list, tree, and hash table, then I suggest you first go through a comprehensive course on Data Structure like Data Structures and Algorithms: Deep Dive Using Java on Udemy. It's essential for every programmer to have a solid understanding of these data structures as they are the basis of writing programs.
1. What is Tree Data Structure?
A tree data structure is a hierarchical data structure that allows you to represent information in a hierarchy. It's most suited for storing information that can be segregated in different levels, and it's derived from the Tree itself.
The only difference between a normal Tree and a Tree data structure is that root is at the top of the tree in the data structure, while in the real tree, it's at the bottom. So, you can say that a Tree data structure is like an inverted tree.
The best thing about a Tree data structure is that you can insert, delete, and search values in logarithmic time. In other words, the average time complexity of insertion, deletion, and searching in a binary tree is O(logN)
Here is an example of a tree data structure in programming:
A binary tree is a tree where each node can have at most 2 children like they can have zero, one, or two children. If they don't have any children, then they are known as leaf nodes.
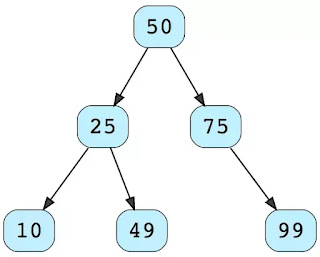
Here is an example of a binary tree data structure, in this case, the root is 50, which has two children, 25 and 75. When you go one level down, node 25 again has two children, 10 and 49, which in turn doesn't have any children. They are called leaf nodes. Similarly, node 75 just has one child, 99, which is a leaf node.
You can see that all node has at most 2 children like node 50 and 25 has two children each, node 75 has one child and nodes 10, 49, and 99 don't have any children.
If you want to learn more about binary tree data structures like how to implement them, different traversal algorithms, and search algorithms, etc. then you can also see Algorithms and Data Structures - Part 1 and 2 courses on Pluralsight. This two-part course is best for anyone starting with data structure and algorithms.
i) The left subtree of nodes can only have values less than the node itself, I mean all nodes in the left subtree will be less than the root.
ii) The right subtree of nodes can only have values greater than the nodes themselves, I mean all nodes in the right subtree will be higher than the root.
iii) No duplicate values are allowed
iv) The left subtree should also be a binary search tree
v) The right subtree should also be a binary search tree
These special properties of the binary search trees make it ideal for searching like you just need to compare the value you want to search with the node, and you almost rule out half of the node from the tree.
This algorithm is known as a binary search, and because of that, the tree is known as a binary search tree. The search only takes log2(N) time which means you can find a node by just comparing 4 values in a binary tree of 16 nodes (log2(16) = 4)
Both Binary tree and Binary Search tree is also a recursive data structure because you take out one node, and the rest of them are still a tree. They are often used to solve recursive problems.
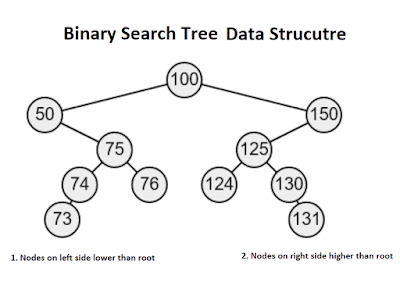
Here is an example of a binary search tree data structure; you can see that each node has at most two children, and nodes on the left side are lower than root, and nodes on the right have values greater than root. If you want to learn more, take Data Structures & Algorithms! Course on Udemy. It's one of the best algorithm courses on Udemy, and it will show you how to insert, delete, and search values on binary search trees along with other problems.
if you inserted nodes in the order {2, 3, 1}, the BST would be O( log(N) ) for searching a node, but if you inserted {1,2,3}, then the BST will be O( N ), like a linked list because all the nodes will be on the right subtree and left subtree will be empty.
A completely un-balanced binary tree is actually a linked list, just like in the above case, and then searching will be O(n) instead of O(logN).
On the other hand, A balanced tree-like AVL or Red-Black tree will reorganize itself so that you will always get O( log(N) ) complexity.
Here is an example of a balanced tree data structure:
A "Red-Black Tree" is a self-balancing Binary Search Tree," with each node marked with a color (either Red or Black) and has additional operations defined on it to maintain "balance."
Some typical applications of Red-black trees are TreeMap and TreeSet in Java. Even the C++ STL library has some collections, like the map, multimap, and multiset, which are based upon a Red-black tree. Linux kernel: entirely fair scheduler, Linux/rbtree.h also uses Red-Black Tree. Though, both provide O(log N) lookup time.
You can further see Algorithms and Data Structures in Python to learn more about the balanced trees in general and the Red-Black Tree in particular.
However, there are the following points of comparison between the two:
AVL trees are more rigidly balanced and hence provide faster look-ups. Thus for a look-up, intensive task, use an AVL tree.
For insert intensive tasks, use a Red-Black tree.
AVL trees store the balance factor at each node. This takes O(N) extra space. However, if we know that the keys that will be inserted in the tree will always be greater than zero, we can use the sign bit of the keys to store the color information of a red-black tree. Thus, in such cases, the red-black tree takes O(1) extra space.
In general, the rotations for an AVL tree are harder to implement and debug than that for a Red-Black tree. There are not many courses that cover this topic well, but Advanced Data Structures in Java - Part I is the best one I found to learn more about AVL trees, Red-Black Trees, and other balanced trees. you should join that course if you are interested in learning more about these advanced data structures.
That's all about the difference between different types of tree data structures. You have learned about the binary tree, binary search tree, and balanced trees like AVL, and Red-Black Tree. We missed one more tree called B-Tree and another important data structure like Trie, but don't worry, we'll cover them in the next article.
We still have covered a lot of ground when it comes to learning tree data structure, and if you want to consolidate that knowledge, I suggest you practice some of the tree-based coding problems from the below lists. If you want to learn more about how to implement these tree data structures like Red-Black Tree, Binary Tree, AVL Tree, Binary Search Tree, etc., check out these recommended courses
Other Binary Tree tutorials in Java for Programmers
Thanks for reading this article so far. If you like this binary tree tutorial, then please share it with your friends and colleagues. If you have any questions or feedback, then please drop a comment.
P. S. - If you are looking for some Free Algorithms courses to improve your understanding of Data Structure and Algorithms, then you should also check these free Data Structure online courses on Udemy. It's authored by a Google Software Engineer and Algorithm expert, and it's completely free of cost.
The only difference between a normal Tree and a Tree data structure is that root is at the top of the tree in the data structure, while in the real tree, it's at the bottom. So, you can say that a Tree data structure is like an inverted tree.
The best thing about a Tree data structure is that you can insert, delete, and search values in logarithmic time. In other words, the average time complexity of insertion, deletion, and searching in a binary tree is O(logN)
Here is an example of a tree data structure in programming:
1. Binary Tree
Now, let's start with the simplest of all tree data structures, the binary tree. You may be wondering, what is a binary tree data structure, and why do we use it? Well, as I said in the previous paragraph, a tree is a hierarchical data structure and hence often used to represent hierarchies, but the binary tree is a little bit special.A binary tree is a tree where each node can have at most 2 children like they can have zero, one, or two children. If they don't have any children, then they are known as leaf nodes.
Here is an example of a binary tree data structure, in this case, the root is 50, which has two children, 25 and 75. When you go one level down, node 25 again has two children, 10 and 49, which in turn doesn't have any children. They are called leaf nodes. Similarly, node 75 just has one child, 99, which is a leaf node.
You can see that all node has at most 2 children like node 50 and 25 has two children each, node 75 has one child and nodes 10, 49, and 99 don't have any children.
If you want to learn more about binary tree data structures like how to implement them, different traversal algorithms, and search algorithms, etc. then you can also see Algorithms and Data Structures - Part 1 and 2 courses on Pluralsight. This two-part course is best for anyone starting with data structure and algorithms.
2. Binary Search Tree
On the other hand, a binary search tree is a binary tree in which node values are assigned by the following rules:i) The left subtree of nodes can only have values less than the node itself, I mean all nodes in the left subtree will be less than the root.
ii) The right subtree of nodes can only have values greater than the nodes themselves, I mean all nodes in the right subtree will be higher than the root.
iii) No duplicate values are allowed
iv) The left subtree should also be a binary search tree
v) The right subtree should also be a binary search tree
These special properties of the binary search trees make it ideal for searching like you just need to compare the value you want to search with the node, and you almost rule out half of the node from the tree.
This algorithm is known as a binary search, and because of that, the tree is known as a binary search tree. The search only takes log2(N) time which means you can find a node by just comparing 4 values in a binary tree of 16 nodes (log2(16) = 4)
Both Binary tree and Binary Search tree is also a recursive data structure because you take out one node, and the rest of them are still a tree. They are often used to solve recursive problems.
Here is an example of a binary search tree data structure; you can see that each node has at most two children, and nodes on the left side are lower than root, and nodes on the right have values greater than root. If you want to learn more, take Data Structures & Algorithms! Course on Udemy. It's one of the best algorithm courses on Udemy, and it will show you how to insert, delete, and search values on binary search trees along with other problems.
3. Balanced Tree (AVL and Red-Black Trees)
Now, let's see what a balanced tree is? Well, A regular Binary Search tree is not self-balancing, which means, depending on the order of insertions, you will get different time complexities. For example;if you inserted nodes in the order {2, 3, 1}, the BST would be O( log(N) ) for searching a node, but if you inserted {1,2,3}, then the BST will be O( N ), like a linked list because all the nodes will be on the right subtree and left subtree will be empty.
A completely un-balanced binary tree is actually a linked list, just like in the above case, and then searching will be O(n) instead of O(logN).
On the other hand, A balanced tree-like AVL or Red-Black tree will reorganize itself so that you will always get O( log(N) ) complexity.
Here is an example of a balanced tree data structure:
4. Red Black Tree
A Red-Black Tree is a self-balancing Binary Search Tree (BST) where every node has the following properties :- Every node has a color, either red or black.
- The root of the tree is always black.
- There are no two adjacent red nodes (A red node cannot have a red parent or red child).
- Every path from the root to a NULL node has the same number of black nodes.
A "Red-Black Tree" is a self-balancing Binary Search Tree," with each node marked with a color (either Red or Black) and has additional operations defined on it to maintain "balance."
Some typical applications of Red-black trees are TreeMap and TreeSet in Java. Even the C++ STL library has some collections, like the map, multimap, and multiset, which are based upon a Red-black tree. Linux kernel: entirely fair scheduler, Linux/rbtree.h also uses Red-Black Tree. Though, both provide O(log N) lookup time.
You can further see Algorithms and Data Structures in Python to learn more about the balanced trees in general and the Red-Black Tree in particular.
5. AVL Trees vs. Red-Black Tree
Now let's see the difference between the Red-Black tree and the AVL tree data structure, Even though, both red-black trees and AVL trees are the most commonly used balanced binary search trees and they support insertion, deletion, and look-up in guaranteed O(logN) time.However, there are the following points of comparison between the two:
AVL trees are more rigidly balanced and hence provide faster look-ups. Thus for a look-up, intensive task, use an AVL tree.
For insert intensive tasks, use a Red-Black tree.
AVL trees store the balance factor at each node. This takes O(N) extra space. However, if we know that the keys that will be inserted in the tree will always be greater than zero, we can use the sign bit of the keys to store the color information of a red-black tree. Thus, in such cases, the red-black tree takes O(1) extra space.
In general, the rotations for an AVL tree are harder to implement and debug than that for a Red-Black tree. There are not many courses that cover this topic well, but Advanced Data Structures in Java - Part I is the best one I found to learn more about AVL trees, Red-Black Trees, and other balanced trees. you should join that course if you are interested in learning more about these advanced data structures.
That's all about the difference between different types of tree data structures. You have learned about the binary tree, binary search tree, and balanced trees like AVL, and Red-Black Tree. We missed one more tree called B-Tree and another important data structure like Trie, but don't worry, we'll cover them in the next article.
We still have covered a lot of ground when it comes to learning tree data structure, and if you want to consolidate that knowledge, I suggest you practice some of the tree-based coding problems from the below lists. If you want to learn more about how to implement these tree data structures like Red-Black Tree, Binary Tree, AVL Tree, Binary Search Tree, etc., check out these recommended courses
Other Binary Tree tutorials in Java for Programmers
- How to implement pre-order traversal in Java? (solution)
- 100+ Data Structure Coding Problems from Interviews (questions)
- How to traverse a binary tree in pre-order without using recursion? (solution)
- 5 Free Data Structure and Algorithms Courses for Programmers (courses)
- How to implement in-order traversal in Java without recursion? (solution)
- 5 Books to prepare data structure and algorithm for programming/coding interviews (list)
- How to implement a binary search tree in Java? (program)
- How to implement in-order traversal in Java? (solution)
- How to implement in-order traversal in Java without recursion? (solution)
- 10 Algorithms Books Every Programmer Should Read (books)
- How to print duplicate elements of an array in Java? (solution)
- How to reverse an array in place in Java? (solution)
- How to reverse a singly linked list in Java? (solution)
- 50+ Data Structure and Algorithms Problems from Interviews (questions)
- 10 Free Data Structure and Algorithm Courses for Programmers (courses)
Thanks for reading this article so far. If you like this binary tree tutorial, then please share it with your friends and colleagues. If you have any questions or feedback, then please drop a comment.
P. S. - If you are looking for some Free Algorithms courses to improve your understanding of Data Structure and Algorithms, then you should also check these free Data Structure online courses on Udemy. It's authored by a Google Software Engineer and Algorithm expert, and it's completely free of cost.




No comments:
Post a Comment
Feel free to comment, ask questions if you have any doubt.