Without any doubt, the array is one of the most used data structures in all programming languages, including Java. Pick up any programming language be it functional, object-oriented, imperative, or even scripting languages like Python, Bash, and Perl, you will always find an array. That's why it's important for any programmer to have a good understanding of the array data structure. Like any other data structure, the array also provides a way to organize and store objects, but the way it does makes all the difference. An array is used to store elements in the contiguous memory location and many C, C++ programmers can take advantage of a pointer to work with an array.
In Java, there are no pointers and arrays are also a little bit different. They are the object, they have a length field that denotes how many elements an array can store. Arrays are created in the special memory area called heap memory in JVM, which is also created when you start the JVM.
What remains the same is that you can access the array element in constant time using their index, this works almost similarly in both C, C++, and Java, they start at index 0 and ends at length -1, but the Java array has an extra caveat that arrays index access are subject to bound check in Java.
In C, it's possible for a program to access an invalid index, mostly an index higher than the size of the array. In Java such attempts will result in ArrayIndexOutOfBoundsException, this is done to protect external memory access from JVM due to malicious programs.
Btw, if you are new to Java and not familiar with fundamental concepts like NullPointerException and ArrayIndexOutOfBoundException, I suggest you go through comprehensive Java courses like The Complete Java MasterClass on Udemy. It will save you a lot of time and also provide you a structured and organized way of learning.
You may know how to iterate through an array using enhanced for loop or how to sort an array using the Arrays.sort() method, but if you don't know fundamentals, it's very unlikely you would be able to write clean and robust code. Even if you know everything about the array in Java, this list may help you to revise some useful details.
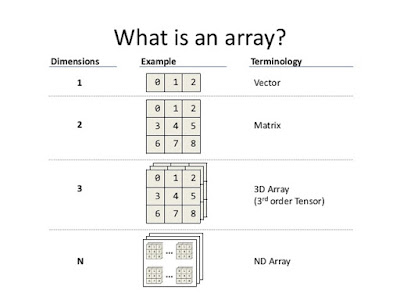
The array data structure can also have more than one dimension and that's why it's very versatile like a one-dimensional array can be used as Vector and a two-dimensional array can be used as Matrix as shown in the following diagram.
If you are not familiar with an array as a data structure and other basic data structures like a linked list, binary tree, and hash table, I also suggest you go through a fundamental data structure and algorithms course like Data Structures and Algorithms: Deep Dive Using Java in Udemy. It will not only help you during your job interviews but also in your day-to-day programming
Well, it's not the resize you think, where you can simply increase the size of an array to accommodate additional elements. In order to increase size, you have to create a new array and copy contents from the old array to a new array.
In Java, there are no pointers and arrays are also a little bit different. They are the object, they have a length field that denotes how many elements an array can store. Arrays are created in the special memory area called heap memory in JVM, which is also created when you start the JVM.
What remains the same is that you can access the array element in constant time using their index, this works almost similarly in both C, C++, and Java, they start at index 0 and ends at length -1, but the Java array has an extra caveat that arrays index access are subject to bound check in Java.
In C, it's possible for a program to access an invalid index, mostly an index higher than the size of the array. In Java such attempts will result in ArrayIndexOutOfBoundsException, this is done to protect external memory access from JVM due to malicious programs.
Btw, if you are new to Java and not familiar with fundamental concepts like NullPointerException and ArrayIndexOutOfBoundException, I suggest you go through comprehensive Java courses like The Complete Java MasterClass on Udemy. It will save you a lot of time and also provide you a structured and organized way of learning.
10 Examples of Array Data Structure in Java
In order to learn and remember some important details about the array data structure in Java, I am sharing these points. These are the things that I believe every Java developer should know about the array.You may know how to iterate through an array using enhanced for loop or how to sort an array using the Arrays.sort() method, but if you don't know fundamentals, it's very unlikely you would be able to write clean and robust code. Even if you know everything about the array in Java, this list may help you to revise some useful details.
1. Array is Object in Java
The first and foremost thing to know is that an array is an object in Java. They are not primitive like int, short, or long, but they are also not a full-featured object with a lot of methods, but because they are objects, they implicitly extend java.lang.Object and that's why you can call any method of java.lang.Object using array reference like toString().The array data structure can also have more than one dimension and that's why it's very versatile like a one-dimensional array can be used as Vector and a two-dimensional array can be used as Matrix as shown in the following diagram.
If you are not familiar with an array as a data structure and other basic data structures like a linked list, binary tree, and hash table, I also suggest you go through a fundamental data structure and algorithms course like Data Structures and Algorithms: Deep Dive Using Java in Udemy. It will not only help you during your job interviews but also in your day-to-day programming
2. The array is a fixed size Data Structure
Another most important thing to know about an array in Java is that once created you can not change the size of the array. Curious developers may ask that then how do we have a dynamic collection like ArrayList in Java, which can resize itself when it gets full?Well, it's not the resize you think, where you can simply increase the size of an array to accommodate additional elements. In order to increase size, you have to create a new array and copy contents from the old array to a new array.
JDK API provides Array.copyOf and Arrays.copyOfRange for that purpose, you can this example to learn more about them.
Though there are fast methods that exist to copy elements from one array to another, it is still an expensive operation and can slow down the performance of your Java application. That's why initializing an array or collection with the proper size is still one of the best practices to follow.
One more thing which increases this confusion is the size() method of ArrayList, which also returns how many elements ArrayList can hold. Here is a sample code snippet to find out the length of an array in Java.
int[] arrayOfInts = new int[] { 101, 102, 103, 104, 105 };
You can use the length of an array while looping through an array in Java to avoid accessing invalid indexes, as shown in the next example.
String[] cities = new String[]{"London", "Paris", "NewYork", "HongKong", "Tokyo"};
For two-dimensional arrays, you get two "[[" e.g. two-dimensional int array has type "[[I". You can check this by yourself when you print an array in Java. It prints its element type and hashcode as shown below.
As I have said before, there is a difference between array as a data structure and array in Java, the former is a concept while the latter is an implementation. If you want to learn more about the array data structure in Java then please check Algorithms and Data Structures - Part 1 and 2 courses on Pluralsight. One of the best resources to learn algorithms and data structure from scratch for beginners and intermediate programmers.
Can we override the toString() method of array class, no that's not an option, but don't worry we have got a utility class java.util.Arrays contain several methods to help with different types of arrays.
You can use the toString() and deep string() method of Arrays class to print elements of an array for one and multi-dimensional array in Java, as shown here.
But don't worry Arrays class got equals() and deepEquals() method to compare elements of one-dimensional and multidimensional arrays in Java. You can infer the same understanding by the following example :
That's all on this list of some important points about the array data structure in Java. Use an array to hold the same type of elements e.g. integers, strings, or objects, but you can not mix them e.g. Java array cannot hold both integer and string at the same time. At compile time it's an error but for objects, if the compiler will allow it will throw ArrayStoreException at runtime.
On the same note, an array is also one of the fasted data-structure for accessing elements if you know the index. Several higher-level data structures like HashMap and HashSet are built on top of the array because of its O(1) get performance.
Though there are fast methods that exist to copy elements from one array to another, it is still an expensive operation and can slow down the performance of your Java application. That's why initializing an array or collection with the proper size is still one of the best practices to follow.
3. Length of Array
The third thing to know about an array is its length property, which tells you the size of an array or how many elements it can hold. It's often a cause of confusion as well because String has a similar length() method, yes that's a method and array length is property, so no more parenthesis.One more thing which increases this confusion is the size() method of ArrayList, which also returns how many elements ArrayList can hold. Here is a sample code snippet to find out the length of an array in Java.
int[] arrayOfInts = new int[] { 101, 102, 103, 104, 105 };
System.out.println("length of arrayOfInts is : " + arrayOfInts.length); // print 5
You can use the length of an array while looping through an array in Java to avoid accessing invalid indexes, as shown in the next example.
4. The first Element in Array is at Index Zero
Array index starts from zero, so the index of the first element is 0 and the index of the last element is length -1. This property is used to iterate over all elements in a loop.String[] cities = new String[]{"London", "Paris", "NewYork", "HongKong", "Tokyo"};
for(int i=0; i<cities.length; i++){
String city = cities[i];
System.out.println("Current city is @ " + city);
}
Output :
Current city is @ London
Current city is @ Paris
Current city is @ NewYork
Current city is @ HongKong
Current city is @ Tokyo
You can see that we are starting the loop from 0 (first element) and ending it less than length e.g. length -1 (last element index). If you try to access array[length], you will get ArrayIndexOutOfBoundsException because the last index is length-1.
5. Type of Array in Java
As I said before that arrays are treated as objects by the Java Virtual Machine. The type of an array is "[elementtype", where element type is the type of the elements. For example, a (1-dimensional) array of integers has the type "[I", similarly a one-dimensional short array has the type "[S", and a one-dimensional float array has the type "[F".For two-dimensional arrays, you get two "[[" e.g. two-dimensional int array has type "[[I". You can check this by yourself when you print an array in Java. It prints its element type and hashcode as shown below.
public class PrintArrayTypes{ public static void main(String args[]) { // type of one dimensional array in Java int[] arrayOfInts = new int[] { 101, 102, 103, 104, 105 }; System.out.println(arrayOfInts); short[] arrayOfShorts = new short[] { 20, 30, 40, 50, 60 }; System.out.println(arrayOfShorts); float[] arrayOfFloats = new float[] { 2.0f, 3.0f, 4.0f, 5.0f, 6.0f }; System.out.println(arrayOfFloats); // type of two dimensional array in Java int[][] arrayOfArrayOfInts = { { 1, 2, 3 }, { 10, 20, 30 }, { 100, 200, 300 } }; System.out.println(arrayOfArrayOfInts); double[][] arrayOfArrayOfDoubles = { { 2.0, 3.0 }, { 4.0, 5.0 } }; System.out.println(arrayOfArrayOfDoubles); } } Output [I@1693b52b [S@3b5b25a1 [F@5d038b78 [[I@7b9a29 [[D@32c5f9fe
As I have said before, there is a difference between array as a data structure and array in Java, the former is a concept while the latter is an implementation. If you want to learn more about the array data structure in Java then please check Algorithms and Data Structures - Part 1 and 2 courses on Pluralsight. One of the best resources to learn algorithms and data structure from scratch for beginners and intermediate programmers.
6. Printing Array in Java
If you have been following my last example, then you will notice that printing an array using toString() will not result in anything useful except that element type. Ideally, we would like to see elements of an array in the order they exist.Can we override the toString() method of array class, no that's not an option, but don't worry we have got a utility class java.util.Arrays contain several methods to help with different types of arrays.
You can use the toString() and deep string() method of Arrays class to print elements of an array for one and multi-dimensional array in Java, as shown here.
7. Arrays.equals() Example
Similar to toString(), equals() method of array is also no use. In most cases, we would like to compare elements of an array and their order to another array and their elements but the equals() method of an array doesn't do that, instead, it does reference comparison and returns true only if both variables are pointing to the same array object, as shown in below example.But don't worry Arrays class got equals() and deepEquals() method to compare elements of one-dimensional and multidimensional arrays in Java. You can infer the same understanding by the following example :
public class ArrayEquality{ public static void main(String args[]) { String[] cities = new String[]{"London", "Paris", "NewYork", "HongKong", "Tokyo"}; String[] metros = new String[]{"London", "Paris", "NewYork", "HongKong", "Tokyo"}; String[] capitals = cities; // comparing array using == operator System.out.println("cities == metros : " + (cities == metros)); System.out.println("cities == capitals : " + (cities == capitals)); // comparing array using equals() method System.out.println("cities.equals(metros) : " + cities.equals(metros)); System.out.println("cities.equals(capitals) : " + cities.equals(capitals)); // comparing array using Arrays.equals() method System.out.println("Arrays.equals(cities, metros) : " + Arrays.equals(cities, metros)); System.out.println("Arrays.equals(cities, capitals) : " + Arrays.equals(cities, capitals)); } } Output : cities == metros : false cities == capitals : true cities.equals(metros) : false cities.equals(capitals) : true Arrays.equals(cities, metros) : true Arrays.equals(cities, capitals) : true
You can see that the first statement is false even though elements and their orders are the same because the "==" operator only returns true if both variables are pointing to the same array, which is the case in the second equality check.
Similarly equals() method also mimics the behavior of the == operator because the array doesn't override the Object's equals() method whose default behavior is to decide equality based upon the same reference. Arrays.equals() is the right method to check if two arrays are equal in Java or not.
You should always use that for this purpose. You can also see the difference between equals() and == in Java to learn more.
Similarly equals() method also mimics the behavior of the == operator because the array doesn't override the Object's equals() method whose default behavior is to decide equality based upon the same reference. Arrays.equals() is the right method to check if two arrays are equal in Java or not.
You should always use that for this purpose. You can also see the difference between equals() and == in Java to learn more.
8. Equality of Multi-dimensional array in Java - deepEquals()
For checking the equality of two multi-dimensional arrays Java programmers should always use the deepEquals() method, because of even Arrays.equals() method doesn't perform a deep comparison. It only does shallow equality checks. Here is an example to check equality of multi-dimensional array in Java:public class MultiDimensionalArray{ public static void main(String args[]) { int[][] a1 = { {2,4}, {4,6}, {8,10} }; int[][] a2 = { {12,14}, {14,16}, {18,20} }; int[][] a3 = { {2,4}, {4, 6}, {8,10} }; // checking if two multi-dimensional array of same // length but different element equal or not boolean result = Arrays.deepEquals(a1, a2); System.out.println("Does two dimensional array a1 and a2 are equal : " + result); // checking if two multi-dimensional array of same length, // elements equal or not result = Arrays.deepEquals(a1, a3); System.out.println("Does two dimensional array a1 and a3 are equal : " + result); } } Output : Does two dimensional array a1 and a2 are equal : false Does two dimensional array a1 and a3 are equal : true
A multidimensional array, the particularly two-dimensional array is used as a Matrix in a lot of problems like matrix addition, matrix multiplication, etc. If you have difficulty with visualizing the 2D array in Java, here is a diagram to remember it.
Similarly, boolean array by default initialized with false values, and String arrays are initialized with null values. If you know the values in advance you can initialize the array at the time of creation itself as shown below:
int[] numbers = {1, 2, 3, 4, 5}; // valid
Apart from this very fact, there are several other differences between these two classes like ArrayList is part of the Java Collection framework but Array is not. See here to learn several more differences between Array and ArrayList in Java.
9. Array to List in Java
While working in Java, you will need to convert between a static array to a dynamic array or ArrayList to an array multiple times. It's good to know how you can do that quickly and this tip will help you a lot.10. Initializing Array in Java
there are several ways to initialize arrays in Java. You can either create them without initializing, in that case, all buckets will hold the default value of element type like if you create an empty array and don't initialize it then all buckets will hold zero because that's a default value of integer variable in Java.Similarly, boolean array by default initialized with false values, and String arrays are initialized with null values. If you know the values in advance you can initialize the array at the time of creation itself as shown below:
int[] numbers = {1, 2, 3, 4, 5}; // valid
int multipleOfThree[] = {3, 6, 9, 12, 15}; // validint[] even = new int[]{2, 4, 6, 8, 10}; // valid
11. Array vs ArrayList in Java
One bonus tip is that Array is quite different than ArrayList in the sense that later is a dynamic array, it can resize itself when needed. On the other hand, you can not change the size of the Array once created.Apart from this very fact, there are several other differences between these two classes like ArrayList is part of the Java Collection framework but Array is not. See here to learn several more differences between Array and ArrayList in Java.
That's all on this list of some important points about the array data structure in Java. Use an array to hold the same type of elements e.g. integers, strings, or objects, but you can not mix them e.g. Java array cannot hold both integer and string at the same time. At compile time it's an error but for objects, if the compiler will allow it will throw ArrayStoreException at runtime.
On the same note, an array is also one of the fasted data-structure for accessing elements if you know the index. Several higher-level data structures like HashMap and HashSet are built on top of the array because of its O(1) get performance.
Do you want to master the Array data structure in Java? Here are some useful Array and Data Structure resources to learn more about array data structure :
Thanks for reading this article so far. If you like this ultimate Java Array tutorial and examples then please share them with your friends and colleagues. If you have any questions or feedback then please drop a note.
P. S. - If you are looking to learn Data Structure and Algorithms from scratch or want to fill gaps in your understanding and looking for some free courses, then you can check out this list of Free Algorithms Courses to start with.
- 22 Array Concepts Interview Questions in Java (questions)
- How to create an array from ArrayList of String in Java (tutorial)
- 7 Best Courses to learn Data Structure and Algorithms (courses)
- 20+ String Coding Problems from Interviews (questions)
- How to remove duplicates from an unsorted array in Java? (solution)
- 20+ array-based coding problems from Interviews (Questions)
- 10 Data Structure Courses to Crack Programming Interviews (courses)
- 20+ binary tree-based coding problems (questions)
- How to find all pairs whose sum is equal to a given number in an array? (solution)
- How to reverse an array in place in Java? (solution)
- 10 Algorithms Books Every Programmer Should Read (books)
- 10 Free Data Structure and Algorithm Courses for Beginners (courses)
- Top 20 Searching and Sorting Interview Questions (questions)
- How to make a binary search tree in Java? (solution)
- 50+ Data Structure and Algorithms Interview Questions (questions)
Thanks for reading this article so far. If you like this ultimate Java Array tutorial and examples then please share them with your friends and colleagues. If you have any questions or feedback then please drop a note.
P. S. - If you are looking to learn Data Structure and Algorithms from scratch or want to fill gaps in your understanding and looking for some free courses, then you can check out this list of Free Algorithms Courses to start with.

ArrayIndexOutOfBounds in Java is a way to prevent BufferOverFlow errors, which can cause a malicious program to store something in a memory location which is not guarded. Java doesn't allow BufferOverFlow error to happen and for this it does bounds check on array, no pointers only helps the cause.
ReplyDeleteCouple of more points about Java array, they are homogenous, you cannont store an int into String array, it will compile time error, but an Object array can store anything, but if a String array stores an object other than String it will throw ArrayStoreException at runtime.
ReplyDeleteNice tip on Arrays#equals and #deepEquals methods. Thank you very much.
ReplyDelete