How to code Binary Search Algorithm using Recursion in Java? Example

Hello guys, In the last article, we have seen the iterative implementation of binary search in Java, and in this article, you will learn how to implement binary search using recursion. Recursion is an important topic for coding interviews but many programmers struggle to code recursive solutions. I will try to give you some tips to come up with recursive algorithms in this tutorial. In order to implement a recursive solution, you need to break the problem into sub-problems until you reach a base case where you know how to solve the problem like sorting an array with one element. Without a base case, your program will never terminate and it will eventually die by throwing the StackOverFlowError.

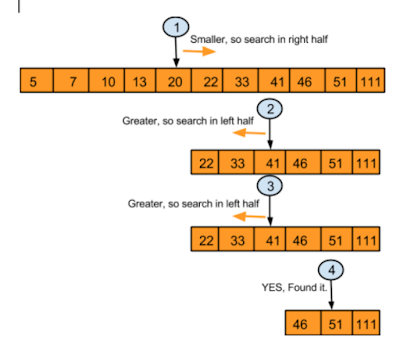
In the case of recursive binary search implementation, we calculate the middle position by taking the start and end position and check if the target element is equal to the middle element or not.

If the target, the number of the element you are searching in an array is equal then our search is complete, but if the target is greater than the middle we look at the second half of the array and if the target is less than the middle element then we look into the first half of array.

This is possible because in the case of binary search the array is always sorted if it's not, you must sort the array before conducting a binary search.

So, in each iteration, the value of start and end position changes like at first, start=0 and end=length-1 but then depending upon the value of the target element we move the pointer to the first or second half of the array.

This gives you the base case I mean,. since the array is getting smaller and smaller in every iteration at one point it will limit to just one element and after that end will be less than the start.

At this point, you can stop the binary search because now you cannot divide the array further, which means the element doesn't exist in the array. Our solution returns -1 at this point in time.

Good knowledge of basic data structure and algorithms also helps to code recursive solutions as most of the linked list and tree-based problems can be solved using recursion. This means you should sharp your algorithms skills as and when possible. If you need a course, I highly recommend Data Structures and Algorithms: Deep Dive Using Java as examples are given in Java programming language which makes it easy to understand them.

Why Recursion? if you already have Iterative Solution?

Now, some of you might ask why should we learn a recursive algorithm if you already know an iterative one? Well, there are many reasons to do it as if you are preparing for the job interview, you must know both solutions because the interviewer prefers candidates who are good at recursion.

Second, recursion is a tricky concept to master and it's in your best interest to learn and master it. There are many programmers who struggle to understand recursion and as per my experience, I have found programmers who understand recursion better are comparative good coders and programmers than those who don't understand a recursive solution or struggle to use recursion in code.

If you are one of them then I strongly suggest you join a comprehensive data structure course like Grokking the Coding Interview: Patterns for Coding Questions on Educative which also explains importing problem-solving techniques like Recursion and Dynamic programming.

If you prefer a book, Grokking Algorithms book by Aditya Bhargava is also a good resource to learn Recursion. It's a visually refreshing book that takes a different and more real-life approach to teach you problem-solving.

Java Program to Implement Binary Search using Recursion

Here is our complete Java solution to implement a recursive binary search. I have a public method recursiveBinarySearch(int[] input, int key), which takes an integer array and a number as a key which we need to search in the array. This method return index of the key if it is found in the array otherwise it returns -1 to indicate that the key doesn't exist in the array.

This method doesn't do anything except accepting parameters from the caller. It then calls the binarySearch(int[] array, int start, int end, int target) which actually performs the binary search.

I have made this method a private method because it's an internal method and should not be exposed to the client or public. This gives you an option to rather switch to a better or iterative algorithm without any change on the client-side because they will keep calling the public recursiveBinarySearch(int[] input, int key) method.

Now the recursive logic is very simple, we calculate the middle index by using the start and end parameters passed to this method, which 0 and length - 1 at the start.

After that, we retrieve the middle element and compare it with the key or target. If it's equal then we return the index otherwise, we repeat the binary search in the first half or second half of the array depending upon whether the key is smaller than the middle element or larger than the key.

To repeat the binary search, we call the same method with a new start and end parameter e.g. start becomes start = middle + 1 if we are searching for the second half of array and end becomes end = middle - 1 if you are searching for the first half of the array. Since we are calling the same binarySearch() method, this solution becomes recursive.

If you want to learn more about recursion and binary search algorithm, you can also join Algorithms and Data Structures - Part 1 and 2 on Pluralsight, one of the most recommended courses to learn Data structure and algorithms. Here is a diagram that nicely explains the recursive binary search algorithm I have described above:

Recursive Binary Search Implementation in Java

Here is our complete Java program to implement a recursive solution to the binary search problem. You can simply run this program from your IDE like Eclipse or IntellijIDEA or you can also run this from the command prompt using java command. Just copy the code and save it into BinarySearchRecursive.java file and then compile using javac command and run using java command.

import java.util.Scanner;

/*
 * Java Program to implement binary search algorithm
 * using recursion
 */

public class BinarySearchRecursive {

  public static void main(String[] args) {

     Scanner commandReader = new Scanner(System.in);
     System.out.println("Welcome to Java Program to perform 
                             binary search on int array");
     System.out.println("Enter total number of elements : ");
     int length = commandReader.nextInt();
     int[] input = new int[length];

     System.out.printf("Enter %d integers %n", length);
     for (int i = 0; i < length; i++) {
        input[i] = commandReader.nextInt();
     }

     System.outprintln("Please enter number to be searched
                           in array (sorted order)");
     int key = commandReader.nextInt();

     int index = recursiveBinarySearch(input, key);

     if (index == -1) {
         System.out.printf("Sorry, %d is not found in array %n", key);
     } else {
         System.out.printf("%d is found in array at index %d %n", key, index);
     }

    commandReader.close();

  }

  /**
  * Java method to perform recursive binary search. It accept an integer array
  * and a number and return the index of number in the array. If number doesn't
  * exists in array then it return -1
  * 
  * @param input
  * @param number
  * @return index of given number in array or -1 if not found
  */
  public static int recursiveBinarySearch(int[] input, int key) {
      return binarySearch(input, 0, input.length - 1, key);
  }

  /**
  * internal method which implement recursive binary search algorithm
  * 
  * @param array
  * @param start
  * @param end
  * @param target
  * @return index of target element or -1 if not found
  */
  private static int binarySearch(int[] array, int start, int end, int target) {
     int middle = (start + end) / 2;
     if (end < start) {
       return -1;
     }

     if (target == array[middle]) {
        return middle;
     } else if (target < array[middle]) {
        return binarySearch(array, start, middle - 1, target);
     } else {
        return binarySearch(array, middle + 1, end, target);
     }
  }

}

Output
Welcome to Java Program to perform binary search on int array
Enter total number of elements : 
3
Enter 3 integers 
10
20
30
Please enter number to be searched in array (sorted order)
30
30 is found in array at index 2 

Welcome to Java Program to perform binary search on int array
Enter total number of elements : 
5
Enter 5 integers 
2
3
4
87
3
Please enter number to be searched in array (sorted order)
4
4 is found in array at index 2 

That's all about how to do the binary search using Recursion in Java. If you did the iterative implementation you will notice that recursive binary search is much simpler than iterative one because the process is naturally recursive. We are repeating the same process again and again and at every iteration, the problem set becomes smaller and smaller, this is the key to the recursive problem.


Other Java Programming exercises for Beginners

• How to calculate the average of all numbers of an array in Java? (program)
• How to implement Linear Search in Java? (solution)
• 50+ Data Structure and Algorithms Coding Problems  (list)
• How to reverse an array in place in Java? (solution)
• How to calculate the sum of all elements of an array in Java? (program)
• 10 Data Structure and Algorithms Courses to Crack Interviews (courses)
• How to remove duplicate elements from the array in Java? (solution)
• How to check if a String contains duplicate characters in Java? (solution)
• How to print Fibonacci series in Java (solution)
• 10 Data Structure and Algorithms Books Every Programmer Read (books)
• How to check if the given String is a palindrome or not in Java? (solution)
• How to reverse a String in place in Java? (solution)
• How to find the highest occurring word from a given file in Java? (solution)
• 20+ String Coding Problems from Interviews (questions)
• How to check if the given number is prime in Java (solution)
• How to check if a year is a leap year in Java? (solution)
• 10 Free Data Structure and Algorithms course for Programmers (courses)
• How to count vowels and consonants in a given String in Java? (solution)
• How to check if two given Strings are Anagram in Java? (solution)
• How to remove duplicate characters from String in Java? (solution)
• How to find all permutations of a given String in Java? (solution)
• How to reverse words in a given String in Java? (solution)
• How to calculate the Area of Triangle in Java? (program)
• How to check if two rectangles intersect with each other in Java? (solution)
• How to calculate the square root of a given number in Java? (solution)
• How to find if given Integer is Palindrome in Java? (solution)

Thanks for reading this article so far. If you like this binary search algorithm tutorial and example then please share with your friends and colleagues. If you have any questions or feedback then please ask, happy to clear any doubt you have. Btw, what is your favorite search algorithm? Linear Search, binary search, breadth first search or depth first search?

P. S. - As I told you if you understand recursion but struggle to come up with a recursive solution reading Grokking Algorithms can help you a lot. There is also an online course called Recursion on Educative which is focused on explaining Recursion in an easy way. You can also take a look at that.